Functional Sets, Part 2: Rotation
Last time we started making a set using a binary search tree. Let’s keep moving!
Quick Recap
We’re modeling binary search trees like this in Elm:
type Set comparable
= Tree comparable (Set comparable) (Set comparable)
| Empty
We can create empty sets using empty, sets from a single item using singleton, and bigger sets by using insert or fromList.
Off Balance
Unfortunately, the insert function we wrote last time has a problem.
It will keep all our values organized, but if you insert values in a certain order you get a very inefficient structure back.
The simplest place this happens is when you try to create a set from a list that’s already in order.
When we run fromList [1, 2, 3, 4, 5] we’d want to get this:
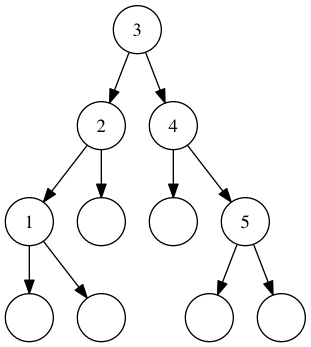
A balanced tree containing the numbers 1 through 5.
But instead, we get:
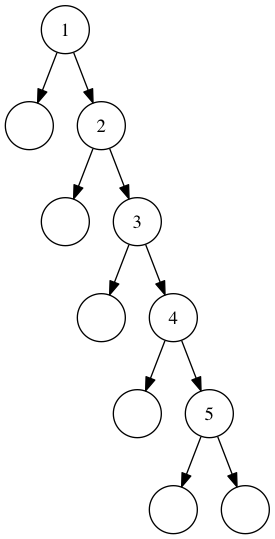
An unbalanced tree, the result of our naïve insert implementation
Think about how we’d retrieve 5 from these sets.
In the nice balanced tree above:
- We’d see that the head is 2.
- Ok, so look in the right subtree, where the head is 4.
- 5 is greater than 4, so right subtree again, and we’ve found it.
Three steps, not terrible. But what about the unbalanced tree?
- The head is 1, so look in the right.
- The next head is 2, so look in the right.
- The next head is 3, so look in the right.
- You get the point. Right again.
- Finally, we find our 5.
So three steps versus five. That doesn’t make a huge difference for small sets, but imagine if you had 1,000 items in your set… you don’t want to look through all of them!
It turns out that for balanced trees, looking up an item in a set of size n takes log2(n) operations.
For a set of 1,000 items, that means about 10 operations instead of 1,000.
This is a huge difference!
So, to get the benefits, let’s make sure that our data structure stays balanced. We’ll do this by rotating our tree!
Tree Rotation
Tree rotation means rearranging the values in a tree in a way that preserves order, but changes the relative height of each side of the tree. Wikipedia has an amazing GIF to explain it:
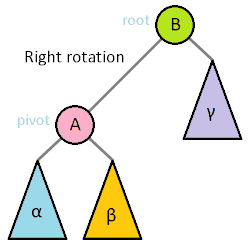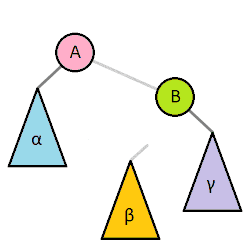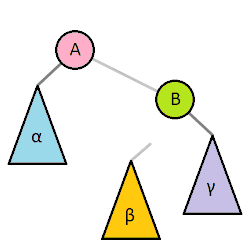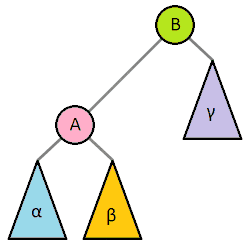
A Tree Rotating Left and Right Wikipedia
In words: to rotate left, we have to have a tree with a non-empty subtree as it’s right subtree.
For the sake of clarity, we’re going to call the original head head and the subtree’s head subHead.
Remember how all the values to the left of a subtree are less than the head, and the values to the right are greater?
Well, that means that the left subtree of the right subtree (the yellow B in the graphic above) contains values between the two heads!
We’ll use that property to our advantage here.
Let’s refer to the left subtree of the original tree as lessThans, and the left and right subtrees of the subtree as betweens and greaterThans.
Now that we’ve got a plan, let’s rotate left (right is just reversing this.)
We’ll create a new Tree, with subHead as the head.
The left subtree will be another new tree, with head as the head, lessThans as the left subtree, and betweens as the right subtree.
Last, we attach greaterThans as the right subtree.
Whew! That’s a ton of words to describe something that’s fairly succinct in code:
rotateLeft : Set comparable -> Set comparable
rotateLeft set =
case set of
Tree head lessThans (Tree subHead betweens greaterThans) ->
tree subHead (tree head lessThans betweens) greaterThans
_ ->
set
rotateRight : Set comparable -> Set comparable
rotateRight set =
case set of
Tree head (Tree subHead lessThans betweens) greaterThans ->
tree subHead lessThans (tree head betweens greaterThans)
_ ->
set
We always put lessThans, betweens and greaterThans in order in the source.
If these ever get out of order, we’re going to be breaking our guarantees about structure!
Next time, we’ll fgure out how to apply these rotations automatically. But for now…
Make Your Own Trees!
It can be really difficult to get all this in your head. When I was learning this, it really helped to visualize it. So, here’s a program that you can use to do the same!
Enter any string value in the box below, and you’ll see the output of our sets so far. Purple circles indicate empty sets, and you can rotate the tree left and right.
Things to try:
- Enter 1, 2, and 3 as the values. Rotate the tree and see how that works.
- Enter 2, 3, 1 in order. Hey, the insert code does what we said it would!
- Enter a through z. Trace the operations you’d take to get to any given letter.