Functional Sets, Part 7: Filter, Diff, and Intersect
This time, let’s look at filter.
It does the same thing as List.filter, except it operates on a Set instead of a List.
We’ll have it take a function that checks whether we should include a value and use the output of that function to filter the values from the set.
We can’t remove values at random without unbalancing our sets, so we’ll use foldl with insert to keep our set balanced:
filter : (comparable -> Bool) -> Set comparable -> Set comparable
filter cmp set =
foldl
(\item acc ->
if cmp item then
insert item acc
else
acc
)
empty
set
We’re inserting the item into a new set if the comparator function returns True, otherwise we’ll skip adding it and return the accumulator value.
Easy enough!
We could implement this in reverse: we’d start with the accumulator as our initial value and use remove if the comparator function didn’t match.
Both approaches work, but in the real world we would benchmark before deciding.
So how do we use filter?
Say we had a set with the numbers 1 through 10:
numbers : Set Int
numbers =
List.range 1 10 |> fromList
If we wanted to get only the even numbers from that set, we’d use filter like this:
evens : Set Int
evens =
filter (\i -> i % 2 == 0) numbers
Bonus: partition
With filter done, we can add partition.
We use this when we want to split a set in two according to some criteria.
It takes the same filter function, but returns both items which passed and failed the filter.
partition : (comparable -> Bool) -> Set comparable -> ( Set comparable, Set comparable )
partition cmp set =
foldl
(\item ( yes, no ) ->
if cmp item then
( insert item yes, no )
else
( yes, insert item no )
)
( empty, empty )
set
intersect
How about we do something more interesting with filter?
We can implement two more combination functions, intersect and diff.
Last week we implemented union.
We can represent that operation as a Venn diagram.
The two circles below represent our two sets, with the shared area representing shared values.
When we take a union of the two sets, we get everything contained in both sets.
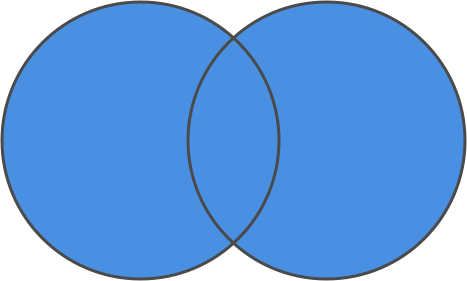
set union
Taking the intersection of the two sets, on the other hand, means taking all the values that the two sets have in common. The circles in our Venn diagram overlap for these values.
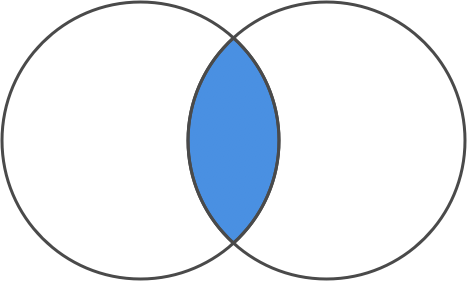
set intersection
The code look like this:
intersect : Set comparable -> Set comparable -> Set comparable
intersect a b =
filter (\item -> member item a) b
We use filter to implement intersect.
We select which items to include by using member.
This can read “if both set a and b have this item, include it.”
That works out to the intersection of the sets!
In pseudocode:
intersect [1, 2] [2, 3] == [2]
diff
But what if we want only the values in one set or the other, instead of both?
To do that, we use diff.
diff removes all the items in the second set from the first set.
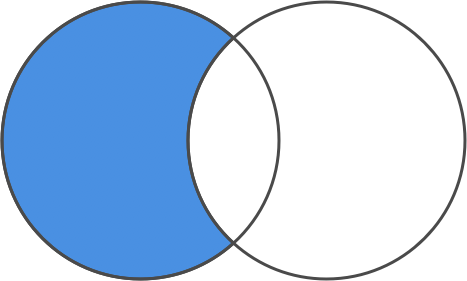
set difference
Do note that we’re implementing an asymmetric diff.
That means that we’re only removing values from one set, in this case the first/left one.
Some set implementations (like most image editing programs) refer to this as subtraction (where union is addition.)
They refer to diff as a symmetric diff, which removes any items in common between the two sets, and leaves only items unique to one or the other.
Elm’s built-in Set uses asymmetric diffs, with the second set removing values from the first. We’ll do that too!
diff : Set comparable -> Set comparable -> Set comparable
diff a b =
filter (\item -> not <| member item b) a
This looks like intersect, but with an added not.
We’re checking if the set b has an item from set a.
If so, we don’t include it.
It ends up working like this, in psuedocode:
diff [1, 2] [2, 3] == [1]
Wrap Up
So we’ve learned:
- You can use folds to implement every collection operation.
filteris no exception. partitiondoes the same thing asfilter, but keeps the items that fell through the filter in a separate set.intersectanddiffusefilter. We wouldn’t have to do this (we could implement using folds every time) but usingfiltermakes things much cleaner.
After this, we have one major piece of the API left: mapping. See you then!